
06 June 2020, Saturday
In this note, we derive the backpropagation algorithm that underlies most deep neural networks.
Let us describe the building blocks of an artificial neuron and the connections it has with other neurons. We shall then derive the backpropagation algorithm for updating the weights of the incoming connections to the neurons during training.
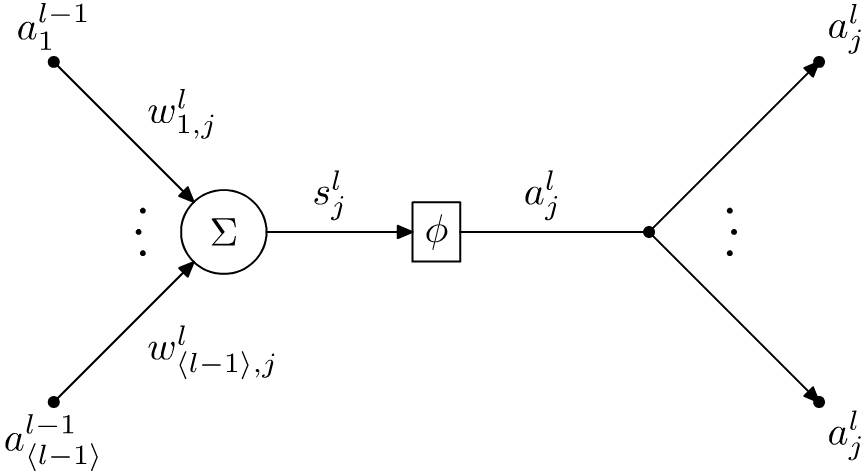
Figure 1.1 shows an abstraction of an artificial neuron. This abstraction is based on the model first suggested by Warren S. McCulloch and Walter Pitts [in “A logical calculus of the ideas immanent in nervous activity,” The Bulletin of Mathematical Biophysics, 5.4 (1943), pp. 115–133. doi: 10.1007/bf02478259]. The figure shows the \(j\)th neuron in the \(l\)th layer. It has two main components. The first is the accumulator, which is denoted with \(\Sigma\). This calculates the weighted sum of the inputs to the neuron. This sum is denoted by \(s_j^l\), meaning the weighted sum calculated by the \(j\)th neuron in the \(l\)th layer. In a fully connected neural network, each neuron is connected to the output of all of the neurons in the previous layer. These outputs are denoted with \(a_j^l\), which means output of the \(j\)th neuron in the \(l\)th layer. In order to calculate the weighted sum, each neuron assigns a weight to each of the inputs. These are denoted with \(w_{i,j}^l\), which means the weight assigned by the \(j\)th neuron in the \(l\)th layer to the output of the \(i\)th neuron in the previous \((l-1)\)th layer. The calculated weighted sum is then passed to the activation function \(\phi\), which is a non-linear function that adds non-linearity to the neural network. Furthermore, the activation function also squashes the output within a range of values before they are used by the neurons in the following layer. We use \(\langle l \rangle\) to denote the cardinality of the layer \(l\), which is the number of neurons in the \(l\)th layer. Hence,
\[ \begin{align} s_j^l = \sum_{i=1}^{\langle l-1 \rangle}w_{i,j}^l.a_i^{l-1}\textrm{ and }a_j^l = \phi(s_j^l).\label{eqn:sum and activation} \end{align} \]
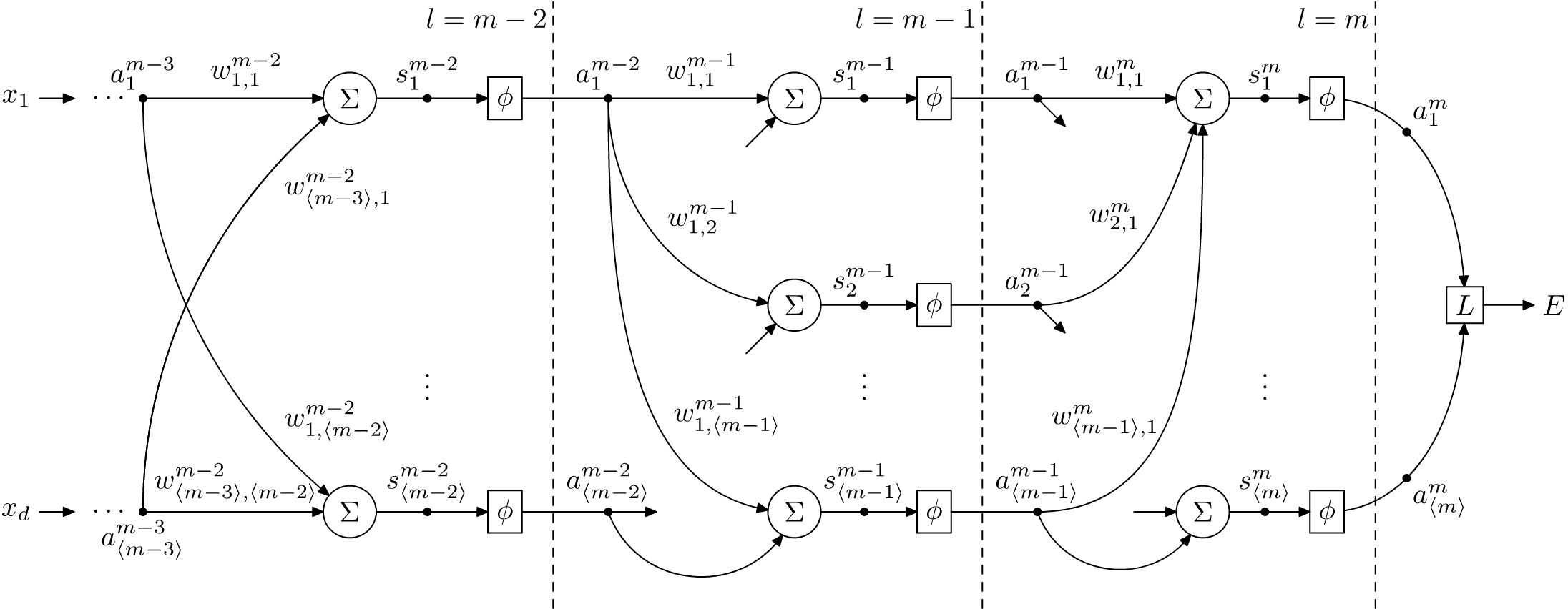
Figure 1.2 shows a multi-layered fully-connected neural network, which uses neurons discussed in the previous section. The neural network shown here has \(m\) layers, and we have shown only the last three layers closer to the output. These layers are indexed \(m\), \((m-1)\) and \((m-2)\) respectively, starting from the output, and moving towards the input values (the input features to train against) from the sample. Each sample used for training the neural network consists of \(d\) coordinates \(x_i\), where \(i = 1,\ldots,d\), shown leftmost. The output produced by the last layer is denoted with \(a_j^m\), where \(j=1,\ldots,\langle m \rangle\). This is used by the loss function denoted \(L\) to calculate the classification error, denoted \(E\). We shall discuss loss functions in another article. Essentially, the loss function evaluates the performance of the neural network by comparing the output \(a_j^m\) against the correct labels assigned to the sample. These correct labels are the ground truth, and they are supplied as part of the supervised training setup.
During training and evaluation, for every sample that is given to the neural network, the neurons in a given layer calculate their output using the supplied input \(x_i\) (if the neuron belongs to the first layer), or using the output of the neurons in the previous layer, for all of the neurons in the following layers. In other words, we start with the first layer, and process each layer sequentially one after the previous until we reach the final output layer. This constitutes one feedforward pass. Hence, for each sample with inputs \(x_i\), we will get a set of outputs \(a_j^m\).
If we were training the neural network, we will use the output to calculate \(E\) using \(L\), and use this to update the weights to minimise \(E\) for this sample. We will then repeat the process for all of the samples in the training data until the error \(E\) has been minimised to an acceptable degree for all samples in the training dataset.
On the othe hand, if we are using the network for inference during evaluation or deployment, the output of the feedforward pass can be converted to a probability distribution (using a softmax layer), which we can then convert to the required output. For instance, we can apply a threshold to convert the distribution to, say, a classification (assuming the final layer produces output that was trained against one-hot encoded ground truth). We shall discuss these other components in separate articles.
During supervised training, we are given a set \(X\) of input samples and the corresponding set of labels \(Y\) to train against. The set \(X\) consists of \(N\) training samples, each defined by \(d\) coordinates \(x_i\) (the features to train against).
Before the training can begin, all of the neurons in the neural network assigns initial weights to its connections. We shall discuss how this is done in a separate article. Using this initial weights, each sample in \(X\) is processed using the feedforward pass and the output is compared against the label in \(Y\). Once we have an error \(E\) calculated using the loss function \(L\), we then adjust the weights of the neural network to reduce \(E\). There are several ways in which this updating can happen. If we update the weights immediately after every sample is processed, this is referred to as the online method. On the other hand, we may decide to update the weights after processing a batch of samples. This is referred to as the batch method. Furthermore, we can decide the order in which the samples in \(X\) are processed. For instance, if the samples from \(X\) are chosen randomly, this is referred to as a stochastic process.
Now, since we initialised the weights without having seen the samples in advance (unless you are using pre-trained weights), it is unlikely that we will get the acceptable error \(E\) in the first training run. We will therefore require processing all of the samples in \(X\) multiple times in order to modify the weights sufficiently to minimise \(E\) to the acceptable value. Each training run that updates the weights of the neural network is referred to as an epoch. What actually happens inside an epoch depends on the type of training method we use, for instance, the number of samples in a batch and how the samples are chosen. We shall discuss this in a separate article.
Let us assume that we will update the weights after processing each sample during a feedforward pass. This means, we will be adjusting all of the weights of the network to minimise the error \(E\) for that sample. In order to do this, we need to know how each of the weights in the network affect the output of the final layer, and therefore the error \(E\). Once we know this, we can adjust the weights accordingly.
Given an error \(E\) for a sample, our aim is to determine the rate-of-change of \(E\) with respect to a weight \(w_{i,j}^l\). This is given by the partial derivative of \(E\) with respect to \(w_{i,j}^l\), denoted \(\partial E/\partial w_{i,j}^l\). Of course, to speed up the training we will adjust all of the weights simultaneously, and therefore use the gradient of \(E\) instead. We discuss this in the article Finding direction of steepest ascent.
When we are at the output layer, which is when \(l=m\) as shown in Figure 1.2, calculating the rate-of-change relative to the weights is straightforward. However, since we have two sets of variables that affect the output, i.e., the output of the \((m-1)\)th layer and the weights assigned to these by the neurons in the \(m\)th layer, we will have two sets of partial derivatives. These are \(\partial E/\partial w_{i,j}^m\) and \(\partial E/\partial a_{i}^{m-1}\). Using the chain rule, we can calculate \(\partial E/\partial w_{i,j}^m\) as follows:
\[\frac{\partial E}{\partial w_{i,j}^m} = \frac{\partial E}{\partial a_j^m}\cdot\frac{\partial a_j^m}{\partial s_j^m}\cdot\frac{\partial s_j^m}{\partial w_{i,j}^m}\textrm{ where, }i=1,\ldots,\langle m-1 \rangle\textrm{ and }j=1,\ldots,\langle m \rangle.\]
From \(\eqref{eqn:sum and activation}\), we have \[\frac{\partial s_j^m}{\partial w_{i,j}^m} = \frac{\partial}{\partial w_{i,j}^m}\sum_{i=1}^{\langle m-1 \rangle}w_{i,j}^m\cdot a_i^{m-1} = a_i^{m-1}\] and hence,
\[ \begin{align} \frac{\partial E}{\partial w_{i,j}^m} = \frac{\partial E}{\partial a_j^m}\cdot\frac{\partial a_j^m}{\partial s_j^m}\cdot a_i^{m-1}. \label{eqn:partial e wrt w} \end{align} \]
To derive \(\partial E/\partial a_{i}^{m-1}\), however, requires some work since the output \(a_i^l\) of the \(i\)th neuron in the \(l\)th layer is used by \(\langle l+1 \rangle\) neurons in the \((l+1)\)th layer. There are therefore multiple paths of dependency between \(a_i^l\) and \(E\). We can see this in Figure 1.2, where, for instance, the output \(a_1^{m-2}\) of the first neuron in the \((m-2)\)th layer is used by \(\langle m-1 \rangle\) neurons in the \((m-1)\)th layer; the outputs of which are then combined by the \(\langle m \rangle\) neurons in the \(m\)th layer. To account for these multiple paths of dependency, we use the chain rule of partial derivatives for a composite multivariable function. In other words, if \(z=f(y_1,\ldots,y_n)\) and \(y_i = g_i(x)\) for some multivariable function \(f\) on \(n\) variables \(y_i\) and functions \(g_i\) on the variable \(x\), then
\[ \begin{align} \frac{\partial z}{\partial x} = \sum_{i=1}^n\frac{\partial f}{\partial y_i}\cdot\frac{dy_i}{dx}. \label{eqn:partial multivariable} \end{align} \]
From Figure 1.2, we can see that for \(j=1,\ldots,\langle m \rangle\), \(s_j^m=\sum_{i=1}^{\langle m-1 \rangle}w_{i,j}^m\cdot a_i^{m-1}\). Furthermore, \(a_i^{m-1}\) is defined as \(\phi(s_i^{m-1})\), where \(s_i^{m-1}=\sum_{k=1}^{\langle m-2 \rangle}w_{k,i}^{m-1}\cdot a_k^{m-2}\). Thus, \(\partial E/\partial a_{i}^{m-2}\) takes the form as shown in \(\eqref{eqn:partial multivariable}\). We therefore have, \[ \begin{align} \frac{\partial E}{\partial a_i^{m-2}} = \sum_{k=1}^{\langle m-1 \rangle}\frac{\partial E}{\partial s_j^m}\cdot\frac{\partial s_j^m}{\partial a_k^{m-1}}\cdot\frac{\partial a_k^{m-1}}{\partial s_k^{m-1}}\cdot\frac{\partial s_k^{m-1}}{\partial a_i^{m-2}}. \label{eqn:partial derivate e wrt a} \end{align} \]
From \(\eqref{eqn:sum and activation}\), we have \[\frac{\partial s_k^{m-1}}{\partial a_i^{m-2}} = w_{i,k}^{m-1}\] and from the chain rule, \[\frac{\partial E}{\partial s_j^m}\cdot\frac{\partial s_j^m}{\partial a_k^{m-1}} = \frac{\partial E}{\partial a_k^{m-1}}.\] Hence, we can rewrite \(\eqref{eqn:partial derivate e wrt a}\) as follows: \[\frac{\partial E}{\partial a_i^{m-2}} = \sum_{j=1}^{\langle m-1 \rangle}\frac{\partial E}{\partial a_j^{m-1}}\cdot\frac{\partial a_j^{m-1}}{\partial s_j^{m-1}}\cdot w_{i,j}^{m-1}.\label{eqn:partial derivate e wrt a(m-2) full}\]
As a consequence,
\[ \begin{align} \frac{\partial E}{\partial a_i^{m-1}} = \sum_{j=1}^{\langle m \rangle}\frac{\partial E}{\partial a_j^m}\cdot\frac{\partial a_j^m}{\partial s_j^m}\cdot w_{i,j}^m. \label{eqn:partial derivate e wrt a(m-1) full} \end{align} \]
This means that the rate-of-change of \(E\) due to the output of neurons in a given layer depends on the rate-of-change of \(E\) due to the output of neurons in the following layer. This is why backpropagation works. Although there are several paths of dependency between the output of a given neuron and \(E\), in order to calculate the rate-of-change of \(E\) with respect to that neuron we only need to look at the rate-of-change with respect to the output of neurons in the following layer. Hence, by starting at the output layer and following a backward pass, we can propagate the error to all of the previous layers, thus allowing us to update the weights accordingly.
Since we will be working with matrices, it is important to vectorise the results discussed in the previous section. Vectorisation will also allow us to update all of the weights simultaneously using matrix operations.
Let us store the output of \(\langle l \rangle\) neurons in the \(l\)th layer in the row matrix \(\mathbf{A}^l\) with dimensions \(1\times \langle l \rangle\), such that
\[ \mathbf{A}^l = \begin{bmatrix} a_1^l & a_2^l & \cdots & a_{\langle l \rangle}^l\end{bmatrix}. \]
Hence, the output matrix for the \((m-1)\)th layer is
\[ \mathbf{A}^{m-1} = \begin{bmatrix} a_1^{m-1} & a_2^{m-1} & \cdots & a_{\langle m-1 \rangle}^{m-1}\end{bmatrix} \]
and the output of the previous layer for the first layer will be the coordinates of the input sample, so that
\[ \mathbf{A}^{0} = \begin{bmatrix} x_1 & x_2 & \cdots & x_{d}\end{bmatrix}. \]
Since there are \(\langle m \rangle\) neurons in the \(m\)th layer, we can denote with \(\mathbf{W}^m\) the weights assigned to the output of the \((m-1)\)th layer as follows:
\[ \mathbf{W}^{m} = \begin{bmatrix} w_{1,1}^m & w_{1,2}^m & \cdots & w_{1,\langle m \rangle}^m\\ w_{2,1}^m & w_{2,2}^m & \cdots & w_{2,\langle m \rangle}^m\\ \vdots & \vdots & \ddots & \vdots\\ w_{\langle m-1 \rangle,1}^m & w_{\langle m-1 \rangle,2}^m & \cdots & w_{\langle m-1 \rangle,\langle m \rangle}^m \end{bmatrix}. \]
Here, each column in \(\mathbf{W}^m\) belongs to weights assigned by each neuron in the \(m\)th layer; whereas, each row corresponds to the weights assigned to the output of a neuron in the preceding \((m-1)\)th layer. For example, the first column \(\begin{bmatrix} w_{1,1}^m & w_{2,1}^m & \cdots & w_{\langle m-1 \rangle,1}^m\end{bmatrix}^T\) gives the weights assigned by the first neuron of the \(m\)th layer to the \(\langle m - 1 \rangle\) outputs of the preceding \((m-1)\)th layer. On the other hand, the first row \(\begin{bmatrix} w_{1,1}^m & w_{1,2}^m & \cdots & w_{1,\langle m \rangle}^m\end{bmatrix}\) gives the weights assigned to the output of the first neuron in the \((m-1)\)th layer by the \(\langle m \rangle\) neurons in the \(m\)th layer. Thus, the dimensions of \(\mathbf{W}^m\) is \(\langle m-1 \rangle\times \langle m \rangle\). If we denote the weighted sum calculated by all neurons in the \(m\)th layer with \(\mathbf{S}^m\), we have
\[ \mathbf{S}^m = \begin{bmatrix} s_1^m & s_2^m & \cdots & s_{\langle m \rangle}^m\end{bmatrix} = \mathbf{A}^{m-1}\times \mathbf{W}^m. \]
Now, given the rate-of-change of \(E\) with respect to the outputs of a given layer \(m\), such that
\[ \dfrac{\partial E}{\partial \mathbf{A}^m} = \begin{bmatrix} \dfrac{\partial E}{\partial a_1^m} & \dfrac{\partial E}{\partial a_2^m} & \cdots & \dfrac{\partial E}{\partial a_{\langle m \rangle}^m}\end{bmatrix} \]
we can calculate the rate-of-change of \(E\) with respect to the weighted sums of the given layer as follows
\[ \dfrac{\partial E}{\partial \mathbf{S}^m} = \begin{bmatrix} \dfrac{\partial E}{\partial a_1^m}\cdot\dfrac{da_1^m}{ds_1^m} & \dfrac{\partial E}{\partial a_2^m}\cdot\dfrac{da_2^m}{ds_2^m} & \cdots & \dfrac{\partial E}{\partial a_{\langle m \rangle}^m}\cdot\dfrac{da_{\langle m \rangle}^m}{ds_{\langle m \rangle}^m}\end{bmatrix} \]
so that
\[ \dfrac{\partial E}{\partial \mathbf{S}^m} = \dfrac{\partial E}{\partial \mathbf{A}^m}\odot\dfrac{d \mathbf{A}^m}{d \mathbf{S}^m}. \]
Here, \(\odot\) denotes the Hadamard product, which is the element-wise product.
From \(\eqref{eqn:partial e wrt w}\), we have \[ \dfrac{\partial E}{\partial \mathbf{W}^m} = \begin{bmatrix} \dfrac{\partial E}{\partial a_1^m}\cdot\dfrac{da_1^m}{ds_1^m}\cdot a_1^{m-1} & \cdots & \dfrac{\partial E}{\partial a_{\langle m \rangle}^m}\cdot\dfrac{da_{\langle m \rangle}^m}{ds_{\langle m \rangle}^m}\cdot a_1^{m-1}\\ \vdots & \ddots & \vdots\\ \dfrac{\partial E}{\partial a_1^m}\cdot\dfrac{da_1^m}{ds_1^m}\cdot a_{\langle m-1 \rangle}^{m-1} & \cdots & \dfrac{\partial E}{\partial a_{\langle m \rangle}^m}\cdot\dfrac{da_{\langle m \rangle}^m}{ds_{\langle m \rangle}^m}\cdot a_{\langle m-1 \rangle}^{m-1}\end{bmatrix} \]
so that
\[ \begin{align} \dfrac{\partial E}{\partial \mathbf{W}^m} = (\mathbf{A}^{m-1})^T\times\dfrac{\partial E}{\partial\mathbf{S}^m}.\label{eqn:final partial e wrt weight} \end{align} \]
Equation \(\eqref{eqn:final partial e wrt weight}\) gives the method to determine the update required to the \(m\)th layer weights. If \(\eta\) is the learning rate, then we can update the weights in the \((k+1)\)th epoch using the weights in the \(k\)th epoch as follows:
\[ \mathbf{W}^{(k+1)} = \mathbf{W}^{(k)} - \eta\dfrac{\partial E}{\partial\mathbf{W}^{(k)}}. \]
Finally, from \(\eqref{eqn:partial derivate e wrt a(m-1) full}\), we have
\[ \dfrac{\partial E}{\partial \mathbf{A}^{m-1}} = \begin{bmatrix} \sum\limits_{j=1}^{\langle m \rangle}\dfrac{\partial E}{\partial a_j^m}\cdot\dfrac{da_j^m}{ds_j^m}\cdot w_{1,j}^m & \cdots & \sum\limits_{j=1}^{\langle m \rangle}\dfrac{\partial E}{\partial a_j^m}\cdot\dfrac{da_j^m}{ds_j^m}\cdot w_{\langle m-1 \rangle, j}^m\end{bmatrix} \]
so that
\[ \dfrac{\partial E}{\partial \mathbf{A}^{m-1}} = \dfrac{\partial E}{\partial\mathbf{A}^m}\times(\mathbf{W}^{m-1})^T. \label{eqn:final partial e wrt previous a} \]
We have derived the equations in the previous section in such a way so that we won’t have to change them when processing multiple samples during batch processing. Furthermore, for performance improvement, which we discuss in the article Matrix multiplication, the matrices are organised so that the result of processing each sample occupies a row in the output matrix. If there are \(N\) samples in a training batch \(X\) where each sample has \(d\) coordinates, so that \(x_i^j\) denotes the \(i\)th coordinate of the \(j\)th sample in \(X\), we will have
\[ \begin{align*} \mathbf{X} = \begin{bmatrix} x_1^1 & x_2^1 & \cdots & x_d^1\\ x_1^2 & x_2^2 & \cdots & x_d^2\\ \vdots & \vdots & \ddots & \vdots\\ x_1^N & x_2^N & \cdots & x_d^N\\ \end{bmatrix}. \end{align*} \]
This means that the dimensions of \(\mathbf{A}^l\) and \(\mathbf{S}^l\) will be \(N\times\langle l \rangle\) instead of \(1\times\langle l \rangle\). Furthermore, the corresponding rate-of-change matrices with respect to \(\mathbf{A}^l\) will also have \(N\) rows instead of just one. We can see that the matrix multiplications continue to work in this case.
I am still writing about the history of how the backpropagation algorithm was invented. Once I am done, either this article will be updated, or a separate article will be written on the history. For now, some details are available on Wikipedia.
