Articles • About

GPT-2 parallelisation: embedding with SIMD (part 1)

Gagarine Yaikhom

29 May 2024, Wednesday

Abstract

GPT-2 parallelisation (part 1): token embedding and positional encoding with SIMD

This is the first part summarising my current experiments with large language models, especially GPT-2. The aim is to understand the internals, while also investigating parallelisation strategies using, say SIMD (AVX, SSE), OpenMP multi-threading, and CUDA. We are using Andrej Karpathy’s sequential implementation of GPT-2 as our reference.

Introduction

Please note that these are sketches to understand each component of a Transformer, specifically, GPT-2: what it does, what affects its performance, and what resources are required. Eventually, my plan is to do an integration where each of these components are linked together by optimising (based on lessons learned from these sketches) all of the components so that the whole is made to perform better. This is similar to a Study in Art, where the artist engages with preliminary sketches to understand the subject and the concept, in preparation for a final piece.

Tokenisation

The following Python script, which uses the Hugging Face transformer API, tokenises a string into GPT-2 tokens.

from transformers import AutoTokenizer
tokenizer = AutoTokenizer.from_pretrained("gpt2")
prompt = 'I went to the bank near the river bank'
input_ids = tokenizer(prompt)['input_ids']
tokens = tokenizer(prompt).tokens()
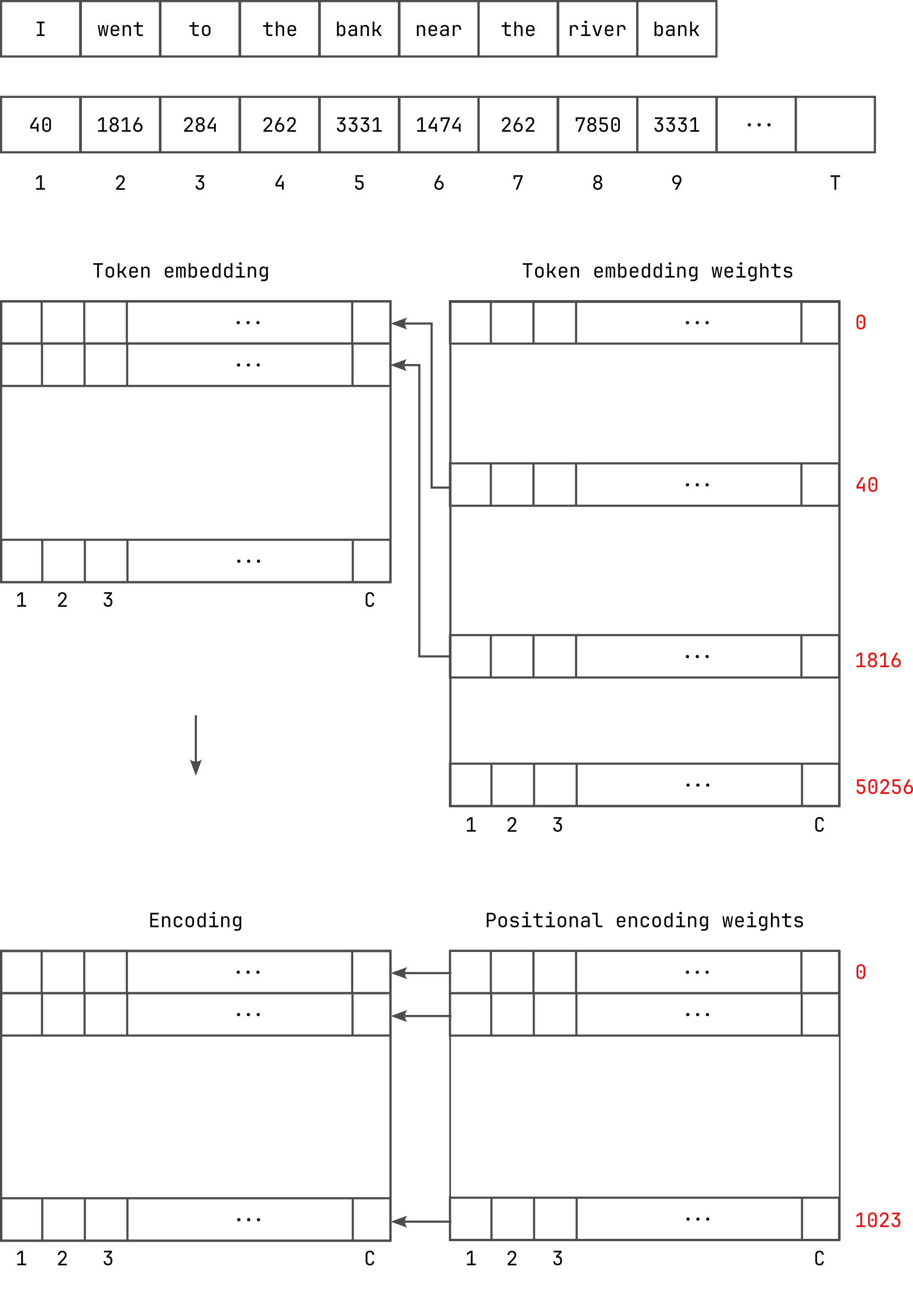
print(f'Token ids: {input_ids}\nTokens: {tokens}\n')

The following is an example tokenisation with the GPT-2 tokeniser, for the sentence:

I went to the bank near the river bank

which produces:

Token ids: [40, 1816, 284, 262, 3331, 1474, 262, 7850, 3331]
Tokens: ['I', 'Ġwent', 'Ġto', 'Ġthe', 'Ġbank', 'Ġnear', 'Ġthe', 'Ġriver', 'Ġbank']

Token embedding and positional encoding

Given the token identifiers, we then do token embedding using a lookup table, where each token is translated to a vector embedding with a specified number of channels (i.e., number of dimensions of the vector space).

Then, we add positional encoding to the token embedding, so that tokens appearing at different locations in the token stream are treated as different. This is important because the position of a word can determine its meaning within that context; for instance, the word bank in our example sentence has different meanings. Although the positional encoding is specified using sampling on sinusoidal waves, these values can be precomputed in advance. Hence, we also do positional encoding using a lookup table.

In our implementation, we will refer to the token embedding weights as wte. This is a two dimensional array of single-precision floating point values, with V rows and C columns. Here, V is the number of unique tokens in the vocabulary (which is 50257 for GPT-2), and C is the number of channels (768 for GPT-2 small). Similarly, we refer to the positional encoding weights as wpe, which is also a two-dimensional array of single-precision floating point values, with T rows and C columns. Here, T is the maximum number of tokens allowed as input to the transformer, which is 1024 for GPT-2 small.

Both wte and wpe are loaded from the GPT-2 model file (as discussed in GPT-2 parameter layout in memory).

GPT-2 parameter layout in memory

The GPT-parameters can be loaded by following the instructions here: https://github.com/karpathy/llm.c In the following, we have changed the variables names a bit to make it consistent with parts to follow:

Sequential implementation

The following is a sequential implementation of token embedding and positional encoding (albeit, with the option to use OpenMP automatic parallelisation when OpenMP multi-threading is available).

void embed_line_of_tokens_seq(
        float * restrict embedding,
        const uint32_t * restrict line,
        const float * restrict wte,
        const float * restrict wpe,
        uint32_t num_tokens,
        uint32_t num_channels
)
{
#pragma omp parallel for                       \
        firstprivate(num_tokens, num_channels, \
                line, wte, wpe, embedding)
        for (uint32_t i = 0; i < num_tokens; ++i) {
                const uint32_t token = line[i];
                const uint32_t idx = i * num_channels;
                const float *t_ptr = wte + token * num_channels;
                const float *p_ptr = wpe + idx;
                float *e_ptr = embedding + idx;

                for (uint32_t j = 0; j < num_channels; ++j)
                        *e_ptr++ = *t_ptr++ + *p_ptr++;
        }
}

Vectorisation using SIMD

To vectorise the implementation, we first do all we can with AVX intrinsics, which processes 8 channels at a time, followed by SSE intrinsics that processes 4 channels at a time, finally processing the remaining channels using scalar instructions. One question that arises when implementing this is, should we use counter or pointer arithmetic? The implementation with pointer arithmetic is:

#if defined(__AVX__)
#if defined(USE_POINTER_ARITHMETIC)
static inline void embed_line_of_tokens_avx(
        float * restrict embedding,
        const uint32_t * restrict line,
        const float * restrict wte,
        const float * restrict wpe,
        uint32_t num_tokens,
        uint32_t num_channels
)
{
        uint32_t num_seq = num_channels;
        const uint32_t num_avx_iters = num_seq >> 3;
        const uint32_t num_avx_items = num_avx_iters << 3;

        num_seq -= num_avx_items;
        const uint32_t num_sse_iters = num_seq >> 2;
        const uint32_t num_sse_items = num_sse_iters << 2;

#pragma omp parallel for                       \
        firstprivate(num_tokens, num_channels, \
                num_avx_items, num_sse_items,  \
                line, wte, wpe, embedding)
        for (uint32_t i = 0; i < num_tokens; ++i) {
                const uint32_t token = line[i];
                const uint32_t idx = i * num_channels;
                const float *t_ptr = wte + token * num_channels;
                const float * const t_end = t_ptr + num_channels;
                const float * const t_avx_end = t_ptr + num_avx_items;
                const float * const t_sse_end = t_avx_end + num_sse_items;
                const float *p_ptr = wpe + idx;
                float *e_ptr = embedding + idx;

                while (t_ptr != t_avx_end) {
                        _mm256_storeu_ps(
                                e_ptr,
                                _mm256_add_ps(
                                        _mm256_loadu_ps(t_ptr),
                                        _mm256_loadu_ps(p_ptr)
                                )
                        );
                        t_ptr += 8;
                        p_ptr += 8;
                        e_ptr += 8;
                }

                while (t_ptr != t_sse_end) {
                        _mm_storeu_ps(
                                e_ptr,
                                _mm_add_ps(
                                        _mm_loadu_ps(t_ptr),
                                        _mm_loadu_ps(p_ptr)
                                )
                        );
                        t_ptr += 4;
                        p_ptr += 4;
                        e_ptr += 4;
                }

                while (t_ptr != t_end)
                        *e_ptr++ = *t_ptr++ + *p_ptr++;
        }
}
#endif
#endif

The following uses channel counters:

#if defined(__AVX__)
#if !defined(USE_POINTER_ARITHMETIC)
static inline void embed_line_of_tokens_avx(
        float * restrict embedding,
        const uint32_t * restrict line,
        const float * restrict wte,
        const float * restrict wpe,
        uint32_t num_tokens,
        uint32_t num_channels
)
{
        uint32_t num_seq = num_channels;
        const uint32_t num_avx_iters = num_seq >> 3;
        const uint32_t num_avx_items = num_avx_iters << 3;

        num_seq -= num_avx_items;

        const uint32_t num_sse_iters = num_seq >> 2;
        const uint32_t num_sse_items = num_sse_iters << 2;

        num_seq -= num_sse_items;

#pragma omp parallel for                               \
        firstprivate(num_tokens, num_channels,         \
                num_seq, num_avx_iters, num_sse_iters, \
                line, wte, wpe, embedding)
        for (uint32_t i = 0; i < num_tokens; ++i) {
                const uint32_t token = line[i];
                const uint32_t idx = i * num_channels;
                const float *t_ptr = wte + token * num_channels;
                const float *p_ptr = wpe + idx;
                float *e_ptr = embedding + idx;

                uint32_t j = 0;
                do_avx_iter();
                do_sse_iter();
                do_seq_iter();
        }
}
#endif
#endif

This uses the following macros:

#define do_seq_iter()                           \
j = num_seq;                                    \
while (j--)                                     \
        *e_ptr++ = *t_ptr++ + *p_ptr++;

#if defined(__SSE__)
#define do_sse_iter()                           \
j = num_sse_iters;                              \
while (j--) {                                   \
        _mm_storeu_ps(                          \
                e_ptr,                          \
                _mm_add_ps(                     \
                        _mm_loadu_ps(t_ptr),    \
                        _mm_loadu_ps(p_ptr)     \
                )                               \
        );                                      \
        t_ptr += 4;                             \
        p_ptr += 4;                             \
        e_ptr += 4;                             \
}
#endif

#if defined(__AVX__)
#define do_avx_iter()                           \
j = num_avx_iters;                              \
while (j--) {                                   \
        _mm256_storeu_ps(                       \
                e_ptr,                          \
                _mm256_add_ps(                  \
                        _mm256_loadu_ps(t_ptr), \
                        _mm256_loadu_ps(p_ptr)  \
                )                               \
        );                                      \
        t_ptr += 8;                             \
        p_ptr += 8;                             \
        e_ptr += 8;                             \
}
#endif

Of course, if we only had SSE instructions, then we will use:

#if defined(__SSE__)
static inline void embed_line_of_tokens_sse(
        float * restrict embedding,
        const uint32_t * restrict line,
        const float * restrict wte,
        const float * restrict wpe,
        uint32_t num_tokens,
        uint32_t num_channels
)
{
        uint32_t num_seq = num_channels;
        const uint32_t num_sse_iters = num_seq >> 2;
        const uint32_t num_sse_items = num_sse_iters << 2;
        num_seq -= num_sse_items;

#pragma omp parallel for                                \
        firstprivate(num_tokens, num_seq, num_channels, \
                num_sse_iters, line, wte, wpe, embedding)
        for (uint32_t i = 0; i < num_tokens; ++i) {
                const uint32_t token = line[i];
                const uint32_t idx = i * num_channels;
                const float *t_ptr = wte + token * num_channels;
                const float *p_ptr = wpe + idx;
                float *e_ptr = embedding + idx;

                uint32_t j = 0;
                do_sse_iter();
                do_seq_iter();
        }
}
#endif

These are called as follows:

void embed_line_of_tokens(
        float * restrict embedding,
        const uint32_t * restrict line,
        const float * restrict wte,
        const float * restrict wpe,
        uint32_t num_tokens,
        uint32_t num_channels
)
{
#if defined(__AVX__)
        embed_line_of_tokens_avx(
                embedding, line, wte, wpe, num_tokens, num_channels
        );
#elif defined(__SSE__)
        embed_line_of_tokens_sse(
                embedding, line, wte, wpe, num_tokens, num_channels
        );
#else
        embed_line_of_tokens_seq(
                embedding, line, wte, wpe, num_tokens, num_channels
        );
#endif
}

Pointer arithmetic or counter method

I was curious if either approaches have advantages over the other. From the compilation point-of-view, yes, there are differences in the instructions used. When compiled with pointer arithmetic enabled as follows:

$ gcc -DUSE_POINTER_ARITHMETIC -std=gnu99 -O3 -ffast-math -msse -msse3 -msse4 -mavx -mavx2 -fopenmp -S -fverbose-asm -o avx_ptr.s embedding.c

we get (only the relevant sections from the assembly code)

.L25:
# embedding.c:290:      const float *t_ptr = wte + token * num_channels;
    movl    %r13d, %eax # num_channels, tmp210
    imull   (%r10), %eax    # MEM[(const uint32_t *)_192], tmp210
# embedding.c:290:      const float *t_ptr = wte + token * num_channels;
    movq    40(%rsp), %rcx  # %sfp, wte
# embedding.c:297:      while (t_ptr != t_avx_end) {
    xorl    %r11d, %r11d    # ivtmp.154
# embedding.c:294:      const float *p_ptr = wpe + idx;
    movq    32(%rsp), %rdx  # %sfp, wpe
# embedding.c:295:      float *e_ptr = embedding + idx;
    movq    48(%rsp), %r14  # %sfp, embedding
# embedding.c:290:      const float *t_ptr = wte + token * num_channels;
    leaq    (%rcx,%rax,4), %r12 #, t_ptr
# embedding.c:291:      const float * const t_end = t_ptr + num_channels;
    movq    24(%rsp), %rax  # %sfp, _48
# embedding.c:292:      const float * const t_avx_end = t_ptr + num_avx_items;
    leaq    (%r12,%rdi), %rbx   #, t_avx_end
# embedding.c:291:      const float * const t_end = t_ptr + num_channels;
    leaq    (%r12,%rax), %r8    #, t_end
# embedding.c:294:      const float *p_ptr = wpe + idx;
    movl    %r9d, %eax  # ivtmp.165, ivtmp.165
# embedding.c:293:      const float * const t_sse_end = t_avx_end + num_sse_items;
    leaq    (%rbx,%rsi), %rcx   #, t_sse_end
# embedding.c:294:      const float *p_ptr = wpe + idx;
    salq    $2, %rax    #, _57
# embedding.c:294:      const float *p_ptr = wpe + idx;
    addq    %rax, %rdx  # _57, p_ptr
# embedding.c:295:      float *e_ptr = embedding + idx;
    addq    %r14, %rax  # embedding, e_ptr
# embedding.c:297:      while (t_ptr != t_avx_end) {
    cmpq    %rbx, %r12  # t_avx_end, t_ptr
    je  .L37    #,
    .p2align 4,,10
    .p2align 3
.L30:
    movq    16(%rsp), %rax  # %sfp, _214
    addq    $4, %r10    #, ivtmp.164
    addl    %r13d, %r9d # num_channels, ivtmp.165
    cmpq    %rax, %r10  # _214, ivtmp.164
    jne .L25    #,
    vzeroupper

On the other hand, when compiled without pointer arithmetic (i.e., counter method) as follows:

$ gcc -std=gnu99 -O3 -ffast-math -msse -msse3 -msse4 -mavx -mavx2 -fopenmp -S -fverbose-asm -o avx_inc.s embedding.c

we get (only the relevant sections from the assembly code)

.L25:
# embedding.c:350:      const float *t_ptr = wte + token * num_channels;
    movl    %r15d, %eax # num_channels, tmp218
    imull   (%r10), %eax    # MEM[(const uint32_t *)_145], tmp218
# embedding.c:350:      const float *t_ptr = wte + token * num_channels;
    movq    72(%rsp), %rbx  # %sfp, wte
# embedding.c:355:      while (j--) {
    xorl    %r11d, %r11d    # ivtmp.169
    movl    60(%rsp), %r13d # %sfp,
# embedding.c:350:      const float *t_ptr = wte + token * num_channels;
    leaq    (%rbx,%rax,4), %rcx #, t_ptr
# embedding.c:351:      const float *p_ptr = wpe + idx;
    movq    64(%rsp), %rbx  # %sfp, wpe
# embedding.c:351:      const float *p_ptr = wpe + idx;
    movl    %r8d, %eax  # ivtmp.182, ivtmp.182
    salq    $2, %rax    #, _52
# embedding.c:351:      const float *p_ptr = wpe + idx;
    leaq    (%rbx,%rax), %rdx   #, p_ptr
# embedding.c:352:      float *e_ptr = embedding + idx;
    movq    80(%rsp), %rbx  # %sfp, embedding
    addq    %rbx, %rax  # embedding, e_ptr
# embedding.c:355:      while (j--) {
    testl   %r13d, %r13d    #
    je  .L37    #,
    .p2align 4,,10
    .p2align 3
.L30:
    addq    $4, %r10    #, ivtmp.181
    addl    %r15d, %r8d # num_channels, ivtmp.182
    cmpq    %r10, 48(%rsp)  # ivtmp.181, %sfp
    jne .L25    #,
    vzeroupper

During runtime though these variations did not produce a significance performance difference. Although pointer arithmetic uses more instructions (21 against 18), I feel the pointer arithmetic version less error prone because it allows the same pointer to follow through from AVX to SSE to sequential.

Performance evaluation

In addition to the SIMD speedup, enabling OpenMP makes a significant difference, depending on the number of CPU threads available. We analyse this in the next post: Statistical analysis of performance improvements due to optimisation techniques.

We have not yet addressed GPU parallelisation using CUDA, which we plan to write about eventually.

References

Copyright © 2024 Gagarine Yaikhom