
03 June 2024, Monday
GPT-2 parallelisation (part 3): layer normalisation with SIMD
In this article we parallelise layer normalisation found in a Transformer (such as GPT-2) using SIMD instructions.
This is the third part of the GPT-2 parallelisation series.
Layer normalisation ensures that the input (token embeddings before QKV phase) and subsequent intermediate attention layers, are standardised.
This prevents the learned weights and biases from being affected by sample specific artefacts in the input and intermediate layers. In other words, this allows the Transformer to learn and generalise across the features in the data, rather than focusing on the features within samples.
Layer normalisation is different from batch normalisation. In layer normalisation, we normalise across the channels, so that the channels of a token is first normalised (calculate the \(z\)-score), followed by scaling (weighting) and shifting (add bias). On the other hand, batch normalisation happens along the channels for the entire batch of tokens. In other words, each channel is normalised, scaled and shifted along all tokens in the batch, and we do this separately for each channel.
Layer normalisation can be summarised with the following diagram:
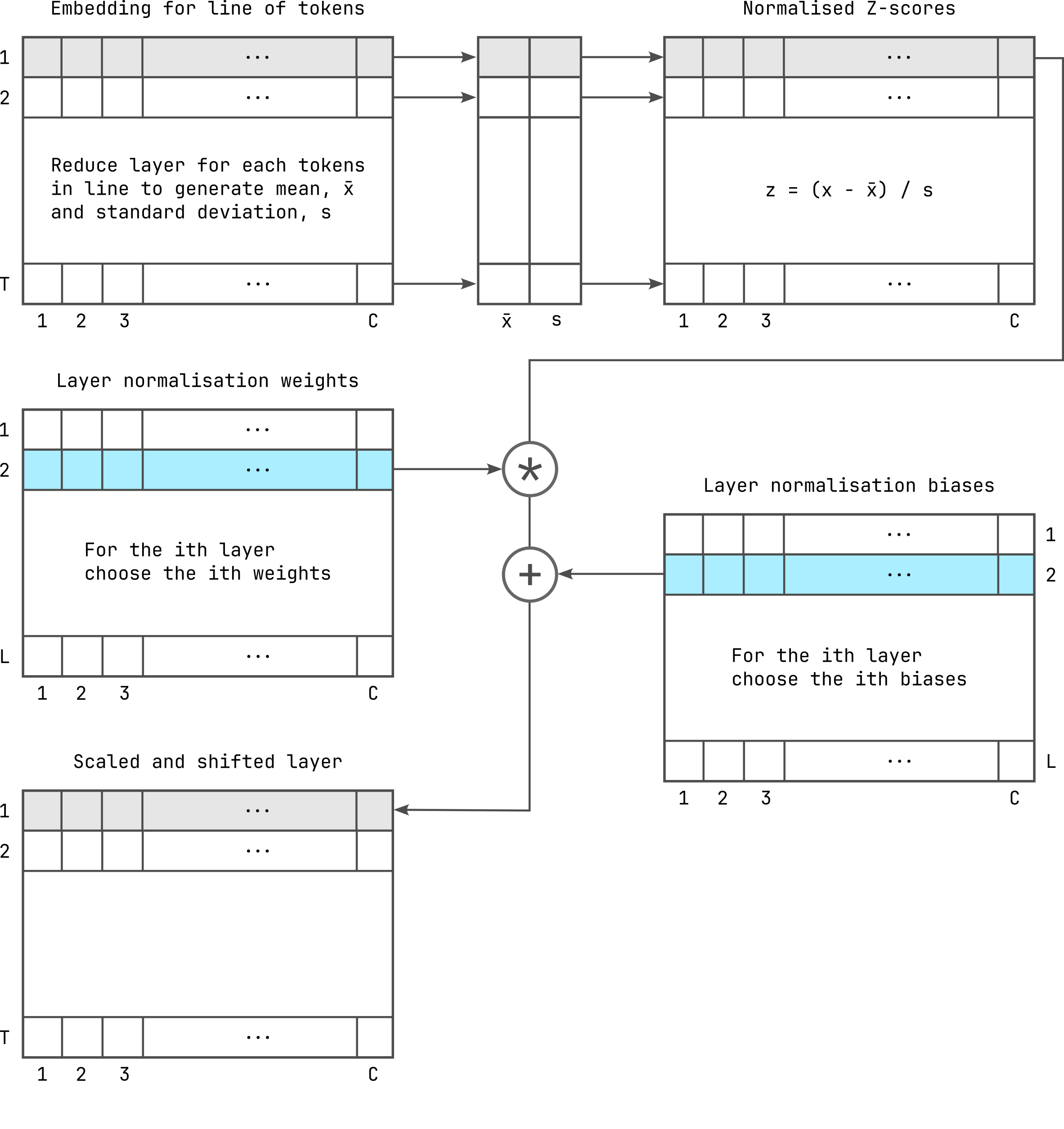
Here, an array of channels is supplied as input. If the layer normalisation is done after the token embedding and positional encoding phase (see GPT-2 parallelisation series), the inputs will be the embedding for a line of tokens, where each line contains \(T\) tokens, and each token is embedded using \(C\) channels. When the input is an intermediate attention layer, these will be the transformed vectors in vector space with \(C\) dimensions.
For each group of channels, we first calculate the sample mean and the biased sample standard deviation (not the unbiased standard deviation, see Why divide by (n-1) when calculating sample variance?). This is the reduction parallel pattern, which we will see frequently in subsequent articles. During reduction, we use multiple threads to reduce an array of values into a single value. For instance, summation, which is required for calculation of the mean, or finding the maximum value, etc. are reduction operations.
Once we have the sample means (\(\bar{x}\)) and standard deviations (\(s\)), we use these to normalise the corresponding group of channels by calculating the \(z\)-scores of the channel values. Hence, for each array of channel values \(x\), we calculate the \(z\)-scores as:
\[z = \frac{x - \bar{x}}{s}.\]
Once we have these, then we scale the channels using the weights and add a bias to shift the channels.
We use different weights and biases depending on the layer we are
normalising. For instance, the layer normalisation after the token
embedding and positional encoding phase is the \(0\)-th layer, such that it uses the first
of the normalisation weights and biases (ln1w and
ln1b, see Memory
layout of GPT-2 parameters).
There are \(L\) weights and biases,
each with \(C\) channels, where \(L\) is the number of layers. Note that
there is a second phase of layer normalisation, which uses a different
set of weights and biases, i.e., ln2w and
ln2b, and a final full-connected layer normalisation, which
uses lnfw and lnfb. All these have the same
number of channels.
The layer normalisation function is implemented as follows:
void layernorm_tokens(
float * restrict output,
float * restrict means,
float * restrict rstds,
const float * restrict input,
const float * restrict weights,
const float * restrict biases,
uint32_t num_channels,
uint32_t num_tokens
)
{
#if defined(__AVX__)
layernorm_tokens_avx(
output, means, rstds, input, weights,
biases, num_channels, num_tokens
);
#elif defined(__SSE__) && defined(__SSE3__)
layernorm_tokens_sse(
output, means, rstds, input, weights,
biases, num_channels, num_tokens
);
#else
layernorm_tokens_seq(
output, means, rstds, input, weights,
biases, num_channels, num_tokens
);
#endif
}The following is a sequential implementation of layer normalisation (albeit, with the option to use OpenMP automatic parallelisation when OpenMP multi-threading is available).
void layernorm_tokens_seq(
float * restrict output,
float * restrict means,
float * restrict rstds,
const float * restrict input,
const float * restrict weights,
const float * restrict biases,
uint32_t num_channels,
uint32_t num_tokens
)
{
#if defined(DEBUG) && !defined(__SSE__)
printf("Cannot print correct floating point values without SSE\n");
#endif
#pragma omp parallel for \
firstprivate(output, means, rstds, input, \
weights, biases, num_channels)
for (uint32_t i = 0; i < num_tokens; ++i) {
uint32_t idx = i * num_channels;
const float *input_ptr = input + idx;
const float *i_ptr = input_ptr;
float sum = 0.0f;
for (uint32_t j = 0; j < num_channels; ++j)
sum += *i_ptr++;
float mean = sum / num_channels;
#if defined(DEBUG) && defined(__SSE__)
if (i == 0)
printf("sum: %.*e\nmean: %.*e\n",
DECIMAL_DIG, sum, DECIMAL_DIG, mean);
#endif
i_ptr = input_ptr;
sum = 0.0f;
for (uint32_t j = 0; j < num_channels; ++j) {
float deviation = *i_ptr++ - mean;
sum += deviation * deviation;
}
float biased_variance = sum / num_channels;
float rstd = 0.0f;
Q_rsqrt(&rstd, biased_variance);
#if defined(DEBUG) && defined(__SSE__)
if (i == 0)
printf("biased_variance: %.*e\nrstd: %.*e\n",
DECIMAL_DIG, biased_variance, DECIMAL_DIG, rstd);
#endif
i_ptr = input_ptr;
float *o_ptr = output + idx;
const float *w_ptr = weights;
const float *b_ptr = biases;
for (uint32_t j = 0; j < num_channels; ++j)
*o_ptr++ = (*i_ptr++ - mean) * rstd *
*w_ptr++ + *b_ptr++;
means[i] = mean;
rstds[i] = rstd;
}
}Since we are experimenting with SIMD instructions, where we enable
and disable SIMD instructions, it was difficult to use the existing C
system libraries to do our experiments, since the installed
sqrtf() function was compiled with SIMD instructions
enabled. Hence, for these experiments we use the fast inverse square
root implementation from the Quake
3D Engine.
/* Quake inverse square root function
* To disable SSE, we cannot use sqrtf() library function. */
void Q_rsqrt(float *output, float input)
{
union {
float f;
uint32_t i;
} conv = { .f = input };
conv.i = 0x5f3759df - (conv.i >> 1);
conv.f *= 1.5F - (input * 0.5F * conv.f * conv.f);
*output = conv.f;
}Similarly, note that we had to disable printing of floating-point values when SSE is disabled, since the C system libraries that I have installed uses SIMD instructions for printing floating-point values.
To vectorise the implementation, we first do all we can with AVX intrinsics, which processes 8 channels at a time, followed by SSE intrinsics that processes 4 channels at a time, finally processing the remaining channels using scalar instructions.
#if defined(__AVX__)
void layernorm_tokens_avx(
float * restrict output,
float * restrict means,
float * restrict rstds,
const float * restrict input,
const float * restrict weights,
const float * restrict biases,
uint32_t num_channels,
uint32_t num_tokens
)
{
uint32_t n = num_channels;
const uint32_t num_avx_blocks = n >> 3;
const uint32_t num_avx_items = num_avx_blocks << 3;
n -= num_avx_items;
const uint32_t num_sse_blocks = n >> 2;
const uint32_t num_sse_items = num_sse_blocks << 2;
#pragma omp parallel for \
firstprivate(output, means, rstds, input, \
weights, biases, num_channels, \
num_avx_items, num_sse_items)
for (uint32_t i = 0; i < num_tokens; ++i) {
const uint32_t idx = i * num_channels;
const float *input_ptr = input + idx;
const float *i_ptr = input_ptr;
const float *i_end = i_ptr + num_channels;
const float *i_avx_end = i_ptr + num_avx_items;
const float *i_sse_end = i_avx_end + num_sse_items;
__m256 sum_avx = _mm256_loadu_ps(i_ptr);
i_ptr += 8;
while (i_ptr != i_avx_end) {
sum_avx = _mm256_add_ps(
sum_avx, _mm256_loadu_ps(i_ptr)
);
i_ptr += 8;
}
__m128 sum_avx_high = _mm256_extractf128_ps(sum_avx, 1);
__m128 sum_avx_low = _mm256_castps256_ps128(sum_avx);
__m128 sum_sse = _mm_add_ps(sum_avx_high, sum_avx_low);
while (i_ptr != i_sse_end) {
sum_sse = _mm_add_ps(sum_sse, _mm_loadu_ps(i_ptr));
i_ptr += 4;
}
sum_sse = _mm_hadd_ps(sum_sse, sum_sse);
sum_sse = _mm_hadd_ps(sum_sse, sum_sse);
float sum = 0.0f;
_mm_store_ss(&sum, sum_sse);
while (i_ptr != i_end)
sum += *i_ptr++;
float mean = sum / num_channels;
#if defined(DEBUG)
if (i == 0)
printf("sum: %.*e\nmean: %.*e\n",
DECIMAL_DIG, sum, DECIMAL_DIG, mean);
#endif
i_ptr = input_ptr;
__m256 mean_avx = _mm256_set1_ps(mean);
__m256 temp_avx = _mm256_sub_ps(
_mm256_loadu_ps(i_ptr),
mean_avx
);
sum_avx = _mm256_mul_ps(temp_avx, temp_avx);
i_ptr += 8;
while (i_ptr != i_avx_end) {
temp_avx = _mm256_sub_ps(
_mm256_loadu_ps(i_ptr),
mean_avx
);
sum_avx = _mm256_add_ps(
sum_avx,
_mm256_mul_ps(temp_avx, temp_avx)
);
i_ptr += 8;
}
sum_avx_high = _mm256_extractf128_ps(sum_avx, 1);
sum_avx_low = _mm256_castps256_ps128(sum_avx);
sum_sse = _mm_add_ps(sum_avx_high, sum_avx_low);
__m128 mean_sse = _mm_set1_ps(mean);
__m128 temp_sse;
while (i_ptr != i_sse_end) {
temp_sse = _mm_sub_ps(
_mm_loadu_ps(i_ptr),
mean_sse
);
sum_sse = _mm_add_ps(
sum_sse,
_mm_mul_ps(temp_sse, temp_sse)
);
i_ptr += 4;
}
sum_sse = _mm_hadd_ps(sum_sse, sum_sse);
sum_sse = _mm_hadd_ps(sum_sse, sum_sse);
_mm_store_ss(&sum, sum_sse);
while (i_ptr != i_end) {
const float deviation = *i_ptr++ - mean;
sum += deviation * deviation;
}
const float biased_variance = sum / num_channels;
float rstd = 0.0f;
Q_rsqrt(&rstd, biased_variance);
#if defined(DEBUG)
if (i == 0)
printf("biased_variance: %.*e\nrstd: %.*e\n",
DECIMAL_DIG, biased_variance, DECIMAL_DIG, rstd);
#endif
i_ptr = input_ptr;
float *o_ptr = output + idx;
const float *w_ptr = weights;
const float *b_ptr = biases;
__m256 rstd_avx = _mm256_set1_ps(rstd);
while (i_ptr != i_avx_end) {
temp_avx = _mm256_sub_ps(
_mm256_loadu_ps(i_ptr),
mean_avx
);
temp_avx = _mm256_mul_ps(temp_avx, rstd_avx);
temp_avx = _mm256_mul_ps(
temp_avx,
_mm256_loadu_ps(w_ptr)
);
_mm256_storeu_ps(
o_ptr,
_mm256_add_ps(
temp_avx,
_mm256_loadu_ps(b_ptr)
)
);
i_ptr += 8;
o_ptr += 8;
w_ptr += 8;
b_ptr += 8;
}
__m128 rstd_sse = _mm_set1_ps(rstd);
while (i_ptr != i_sse_end) {
temp_sse = _mm_sub_ps(_mm_loadu_ps(i_ptr), mean_sse);
temp_sse = _mm_mul_ps(temp_sse, rstd_sse);
temp_sse = _mm_mul_ps(temp_sse, _mm_loadu_ps(w_ptr));
_mm_storeu_ps(
o_ptr,
_mm_add_ps(temp_sse, _mm_loadu_ps(b_ptr))
);
i_ptr += 4;
o_ptr += 4;
w_ptr += 4;
b_ptr += 4;
}
while (i_ptr != i_end)
*o_ptr++ = (*i_ptr++ - mean) * rstd *
*w_ptr++ + *b_ptr++;
means[i] = mean;
rstds[i] = rstd;
}
}
#endifThe SSE only implementation (when AVX in not available) is as follows:
#if defined(__SSE__) && defined(__SSE3__)
void layernorm_tokens_sse(
float * restrict output,
float * restrict means,
float * restrict rstds,
const float * restrict input,
const float * restrict weights,
const float * restrict biases,
uint32_t num_channels,
uint32_t num_tokens
)
{
const uint32_t num_sse_blocks = num_channels >> 2;
const uint32_t num_sse_items = num_sse_blocks << 2;
#pragma omp parallel for \
firstprivate(output, means, rstds, input, \
weights, biases, num_channels, num_sse_items)
for (uint32_t i = 0; i < num_tokens; ++i) {
const uint32_t idx = i * num_channels;
const float *input_ptr = input + idx;
const float *i_ptr = input_ptr;
const float *i_end = i_ptr + num_channels;
const float *i_sse_end = i_ptr + num_sse_items;
__m128 sum_sse = _mm_loadu_ps(i_ptr);
i_ptr += 4;
while (i_ptr != i_sse_end) {
sum_sse = _mm_add_ps(sum_sse, _mm_loadu_ps(i_ptr));
i_ptr += 4;
}
sum_sse = _mm_hadd_ps(sum_sse, sum_sse);
sum_sse = _mm_hadd_ps(sum_sse, sum_sse);
float sum = 0.0f;
_mm_store_ss(&sum, sum_sse);
while (i_ptr != i_end)
sum += *i_ptr++;
float mean = sum / num_channels;
#if defined(DEBUG)
if (i == 0)
printf("sum: %.*e\nmean: %.*e\n",
DECIMAL_DIG, sum, DECIMAL_DIG, mean);
#endif
i_ptr = input_ptr;
__m128 mean_sse = _mm_set1_ps(mean);
__m128 temp_sse = _mm_sub_ps(_mm_loadu_ps(i_ptr), mean_sse);
sum_sse = _mm_mul_ps(temp_sse, temp_sse);
i_ptr += 4;
while (i_ptr != i_sse_end) {
temp_sse = _mm_sub_ps(_mm_loadu_ps(i_ptr), mean_sse);
sum_sse = _mm_add_ps(
sum_sse,
_mm_mul_ps(temp_sse, temp_sse)
);
i_ptr += 4;
}
sum_sse = _mm_hadd_ps(sum_sse, sum_sse);
sum_sse = _mm_hadd_ps(sum_sse, sum_sse);
_mm_store_ss(&sum, sum_sse);
while (i_ptr != i_end) {
const float deviation = *i_ptr++ - mean;
sum += deviation * deviation;
}
const float biased_variance = sum / num_channels;
float rstd = 0.0f;
Q_rsqrt(&rstd, biased_variance);
#if defined(DEBUG)
if (i == 0)
printf("biased_variance: %.*e\nrstd: %.*e\n",
DECIMAL_DIG, biased_variance, DECIMAL_DIG, rstd);
#endif
i_ptr = input_ptr;
float *o_ptr = output + idx;
const float *w_ptr = weights;
const float *b_ptr = biases;
__m128 rstd_sse = _mm_set1_ps(rstd);
while (i_ptr != i_sse_end) {
temp_sse = _mm_sub_ps(_mm_loadu_ps(i_ptr), mean_sse);
temp_sse = _mm_mul_ps(temp_sse, rstd_sse);
temp_sse = _mm_mul_ps(temp_sse, _mm_loadu_ps(w_ptr));
_mm_storeu_ps(
o_ptr,
_mm_add_ps(temp_sse, _mm_loadu_ps(b_ptr))
);
i_ptr += 4;
o_ptr += 4;
w_ptr += 4;
b_ptr += 4;
}
while (i_ptr != i_end)
*o_ptr++ = (*i_ptr++ - mean) * rstd *
*w_ptr++ + *b_ptr++;
means[i] = mean;
rstds[i] = rstd;
}
}
#endifPerformance evaluation and CUDA implementation to be written.
llm.c